이 내용은 회원 전용이므로 로그인해주시기 바랍니다. 회원이 아니시면 아래에서 회원가입해주세요.
인기글
-
 중계기 전원반 설치기준
99 views | posted on 9월 6, 2025
중계기 전원반 설치기준
99 views | posted on 9월 6, 2025
-
 화재 플룸(Fire Plume) 발생원리 구조 실링제트(Ceiling Jet)
75 views | posted on 7월 29, 2025
화재 플룸(Fire Plume) 발생원리 구조 실링제트(Ceiling Jet)
75 views | posted on 7월 29, 2025
-
 무창층 조건과 소방시설 적용대상
61 views | posted on 7월 9, 2024
무창층 조건과 소방시설 적용대상
61 views | posted on 7월 9, 2024
-
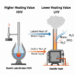 고위발열량과 저위발열량의 차이점, 핵심은 ‘증발잠열’입니다
61 views | posted on 7월 14, 2025
고위발열량과 저위발열량의 차이점, 핵심은 ‘증발잠열’입니다
61 views | posted on 7월 14, 2025
-
 무선통신보조설비 설치대상 구성요소 설치기준
47 views | posted on 7월 22, 2024
무선통신보조설비 설치대상 구성요소 설치기준
47 views | posted on 7월 22, 2024









